A Fisher matrix for gravitational-wave population inference
Published:
Population analyses with gravitational-wave (GW) data are hard and computationally expensive, but crucial for the future of GW astrophysics. In our recent paper, we have taken a step back and thought about alternative ways to estimate the precision on distribution parameters that would better lend themselves to quick and precise forecast estimates.
Table of Content
- Brief description of the formalism
- Predicting the distribution of supermassive black holes
- Validating the prediction
- Final thoughts
Brief description of the formalism
Our approach has been to develop a Fisher Information matrix formalism that can capture the error on hyperparameters of distributions, without going through expensive computational calculations. The Fisher Information is a way of measuring the amount of information a random observable carries about an unknown set of parameters. In our case the random observable is the data streams $d$ gathered by interferometers, which we take to be a combination of Gaussian noise $n(t)$ and a putative signal $h(t,\theta)$,
\[d(t,\theta) = n(t) + h(t,\theta).\]Here $\theta$ is the set of source parameters, namely the parameters that describe the source of the GWs. For instance, these could be the masses and the spins that describe a black-hole binary.
In its most generic form, the Fisher matrix can be defined as the variance of the score, i.e. the partial derivative of the likelihood. Formally, it is defined as the following expectation value,
\[(\Gamma_\theta)_{ij} = E\left(-\frac{\partial^2\ln p(d , \theta )}{\partial\theta^i\partial\theta^j}\right),\]where $p(d, \theta )$ is the likelihood of data $d$ being observed given $\theta$.
The above is the starting point for many source parameter precision forecasts, which have been extensively used to scope out the science case of future experiments such as ESA and NASA’s spaceborn LISA mission, or extension of the LIGO-Virgo-KAGRA networks on the ground.
We ask: can we write an analogous form of the Fisher matrix for distribution hyperparameters?
That is, instead of forecasting the parameters that describe the source, could we describe another hierarchy of parameters that tell us, for instance, how black holes are distributed in the Universe? How far they are? Are they generally spinning or not? All of these questions are the backbone of analyses that aim at discerning the origin of black holes.
In analogy with equation (2) above, we can write the Fisher matrix for hyperparameters as
\[(\Gamma_\lambda)_{ij} = E\left(-\frac{\partial^2\ln p(d , \lambda )}{\partial\lambda^i\partial\lambda^j}\right),\]where $p(d, \lambda )$ is the likelihood of data $d$ being observed given a set of hyperparameters $\lambda$. In the context of GWs, the likelihood of population hyperparameters is combined with priors $\pi (\lambda)$ to get posterior estimates $p( \lambda,d )$ using Bayes theorem,
\[p(\lambda,d ) \propto \pi(\lambda) \prod_{i=1}^n p(d,\lambda).\]The bulk of Sec. II in the paper contains a derivation of an expression for the Fisher matrix for $\lambda,$ starting from $(\Gamma_\lambda)_{ij}$ above. While the final form is rather complex, we find the first term to approximate the full expression well as long as the individual measurements of $\theta$ are well resolved from noise. The approximate expression reads,
\[(\Gamma_{ij})\approx -\int \frac{\partial^2 \ln (p(\theta , \lambda)/P_{\rm det}(\lambda))}{\partial\lambda^i \partial\lambda^j} \, \frac{P_{\rm det}(\theta)}{P_{\rm det}(\lambda)} p(\theta , \lambda) {\rm d} \theta\]where we have introduced $p(\theta,\lambda)$, $P_{\rm det}(\theta)$ and $P_{\rm det}(\lambda)$. The first of these, $p(\theta,\lambda)$, is the probability that a source parameter is drawn given a hyperparameter $\lambda$. In other words, it is the model we pick to draw binaries from a set of hyperparameters.
The other two quantities we have introduced, $P_{\rm det}(\theta)$ and $P_{\rm det}(\lambda)$, represent the selection effects on both the source and hyperparameters. These functions are supposed to dampen our ability to observe certain elements of the population model $p(\theta,\lambda)$ due to our fundamental limitations to observe their parameters. For instance, the masses of the black holes may be at frequencies that our out of the detectors’ band, which prevents us from observing them: in this case, $P_{\rm det}(\theta)$ and $P_{\rm det}(\lambda)$ step in and account for this uncertainty in the overall likelihood. A great treatment of selection effects in GW studies can be found in (Mandel, Gair & Farr, 2018).
Let us now show how the Fisher formalism could be used in the context of GW observations through a specific example in which we estimate the slope of the mass distribution of supermassive black holes.
Predicting the distribution of supermassive black holes
The spaceborne LISA mission is expected to detect extreme mass ratio inspirals (EMRIs), namely binary systems in which one compact object, typically a stellar remnant, has a mass that is much smaller than the companion, typically a supermassive black hole (SMBH) in the centre of a galaxy. Inference of the parameters that characterise EMRI systems is expected to provide accurate constraints on general relativity, as well as an insight into the astrophysical population of and stellar environments surrounding SMBHs.
The use of LISA observations of EMRIs to provide measurements of the BH mass function in the range probed by LISA has previously been investigated in (Gair et al., 2010), where it was assumed that the mass function was described by a power law
\[p(M,\alpha)\propto M^{\alpha-1},\]with a true value for the spectral index $\alpha$ that is close to flat in the log of the masses, i.e., $\alpha \approx 0.$ We note that the above equation is of the form $p(\theta,\lambda)$, where the source parameter $\theta$ is the mass and the hyperparameter $\lambda$ is the spectral index $\alpha$.
(Gair et al., 2010) explored the ability of LISA to constrain the parameters of this mass function, using Markov Chain Monte Carlo (MCMC) techniques to carry out hierarchical analyses on an extensive set of populations of simulated events. They found that with 10 events, $\alpha$ could be constrained at a level of precision $\Delta\alpha = 0.3$.
Here, we will use the population Fisher Matrix formula described above to predict the precision with which a set of EMRI observations might be able to constrain a power-law mass function.
We will assume that events in the population are characterised by a single parameter, the mass, which we measure with our detector with a Gaussian uncertainty that has a fixed variance, independent of the parameters of the source. We draw $N=100$ masses from the power law,
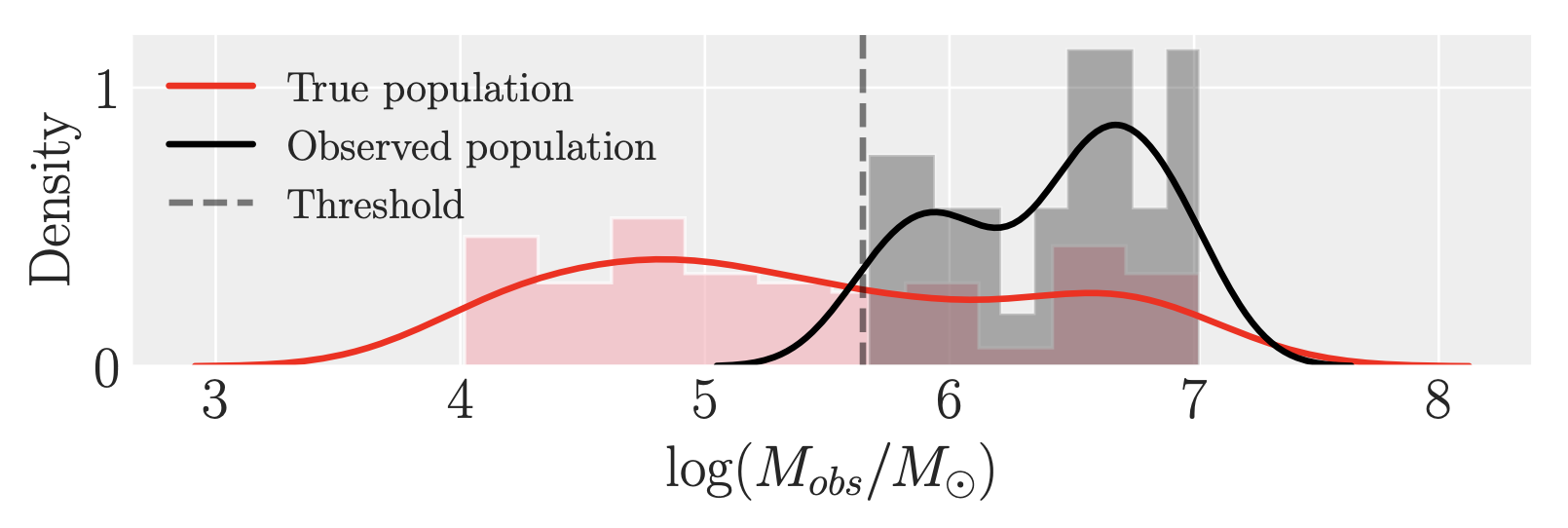
\[p(M|\alpha) = \frac{\alpha}{M^\alpha_\text{max}-M^\alpha_\text{min}} M^{\alpha-1},\]with maximal and minimal observable masses $M_\text{min}=10^4 M_\odot$ and $M_\text{max}=10^7 M_\odot$ (at the frequency-band extrema of LISA). The true value for the spectral index that is taken to be flat in the log of the masses, $\alpha=0$. The observed data is assumed to be a point estimate of the log of the mass, which is equal to the true value plus a normally-distributed uncertainty that has a variance $\sigma =0.1$.
An arbitrary hard cutoff $d_{\text{th}}$ corresponding to masses $M\sim 5\times 10^{5} M_\odot$ is imposed, and only events with observed values above this threshold are included in the analysis. This introduces a large selection effect, and leads to only $N_{\text{det}}=39$ of the original 100 sources being observed.
The distribution of actual and observed masses can be inspected below.
The Fisher-matrix prediction can be obtained from Eq. (5) above. For sufficiently simple models, the integrals are analytically tractable. With the power-law distribution considered here, and in the presence of selection effects, this is already not possible. Because of this, we obtain the Fisher prediction in a semi-analytical fashion by solving the integrals with Monte-Carlo methods, i.e., by generating a sufficiently large set of $N_\text{s}$ samples, ${M_i}$, from a distribution $p(M, \alpha)$, we can approximate the integral of an arbitrary function $X(M)$ via
\[\int X(M) p(M|\alpha)dM\approx \frac{1}{N_\text{s}} \sum_i X(M_i).\]In this case we can draw samples from the power-law distribution directly using the method of inversion. Following this procedure, we find that the Fisher matrix predicts $\Delta \alpha = \sqrt{(N_\text{det}\Gamma_{\alpha})^{-1}}\approx 0.19$. When rescaled to 10 observations by multiplying by $\sqrt{39/10}$, the inferred error is $\Delta \alpha\approx 0.37$, which is in good agreement with what was obtained by (Gair et al., 2010), despite the wild differences in the assumptions used in each case.
Validating the prediction
The successful comparison in the previous paragraph is encouraging, but it cannot be the final word. First of all, (Gair et al., 2010) was published years before a more complete treatment of selection effects was available, which leads to very different assumptions in the hyperparameter inference. Moreover, the analysis is hardly reproducible if we wanted, for instance, to change the source or hyperparameters.
For this reason we have decided to develop our own MCMC analysis. This allows us to validate the Fisher predictions with MCMC estimates for arbitrary datasets, making sure the treatment of selection effects is consistent between the two approaches. We perform the MCMC analysis using $\texttt{emcee}$, which leverages Bayes theorem in equation (4) to get $\Delta\alpha$ independently of the Fisher formalism of equation (5).
As log-likelihood for Eq. (4) we take the sum of log-likelihoods from individual observations, \begin{align} \log p(d,\lambda)=- N_\text{det}\log p_\text{det}(\lambda) + \sum_{i}^{N} \log p(d_i,\lambda), \end{align} We choose flat hyperpriors $\pi (\lambda)$ over a very broad range that includes the true values. The selection function is approximated by a Monte Carlo integral,
\[p_\text{det}(\alpha)=(1/N_\text{s}) \sum \text{erfc}[(d_{\text{th}} - M_i)/\sqrt{2\sigma^2}]/2,\]with $M_i$ drawn from the power law distribution $p(M,\alpha)$.
The posterior, KDE and $2\sigma$ percentile for the estimate of $\alpha$ are shown below.

The MCMC prediction is found to be $\Delta\alpha_{\rm MCMC} = 0.177$, while the Fisher’s is $\Delta\alpha_{\rm Fisher}=0.183$. This shows an excellent agreement, with the latter being only 3% larger than the former prediction. We have repeated the analysis many times in the paper, showing that the formalism works at a similar level or better when $N>10$.
Final thoughts
The Fisher information matrix is a valuable tool for estimating the precision attainable in parameter inference, especially in contexts where the cost of doing full posterior estimation via Bayesian sampling is highly expensive. The Fisher matrix has been widely used in GW analyses to make forecasts for the precision with which the source parameters describing individual GW signals can be estimated by current and future detectors. In this paper we have extended the Fisher matrix concept to the estimation of the parameters characterising the population from which a set of observed sources is drawn.
We conclude that we can reproduce the results of extensive sets of computationally expensive MCMC simulations much more cheaply, while also correctly including selection effects.
The results presented in our paper represent the first attempt at describing population inference within a Fisher formalism for generic population models, and with a likelihood that takes into account selection effects.
The formalism we have developed can be used to obtain forecasts for the precision of population analyses with future ground-based and spaceborne detectors, which are expected to detect many thousands (or even millions) of signals. Obtaining such population inference forecasts in specific contexts of relevance to current and future observations is one possible future direction for the present project.
